Harmonic Oscillator
一维谐振子的相图
横坐标为 $$x=x_0 \cos \omega t \tag{1}$$ 纵坐标为 $$p=-mx_0 \omega \sin \omega t \tag{2}$$
Action-angle 变量 $(I,\theta)$
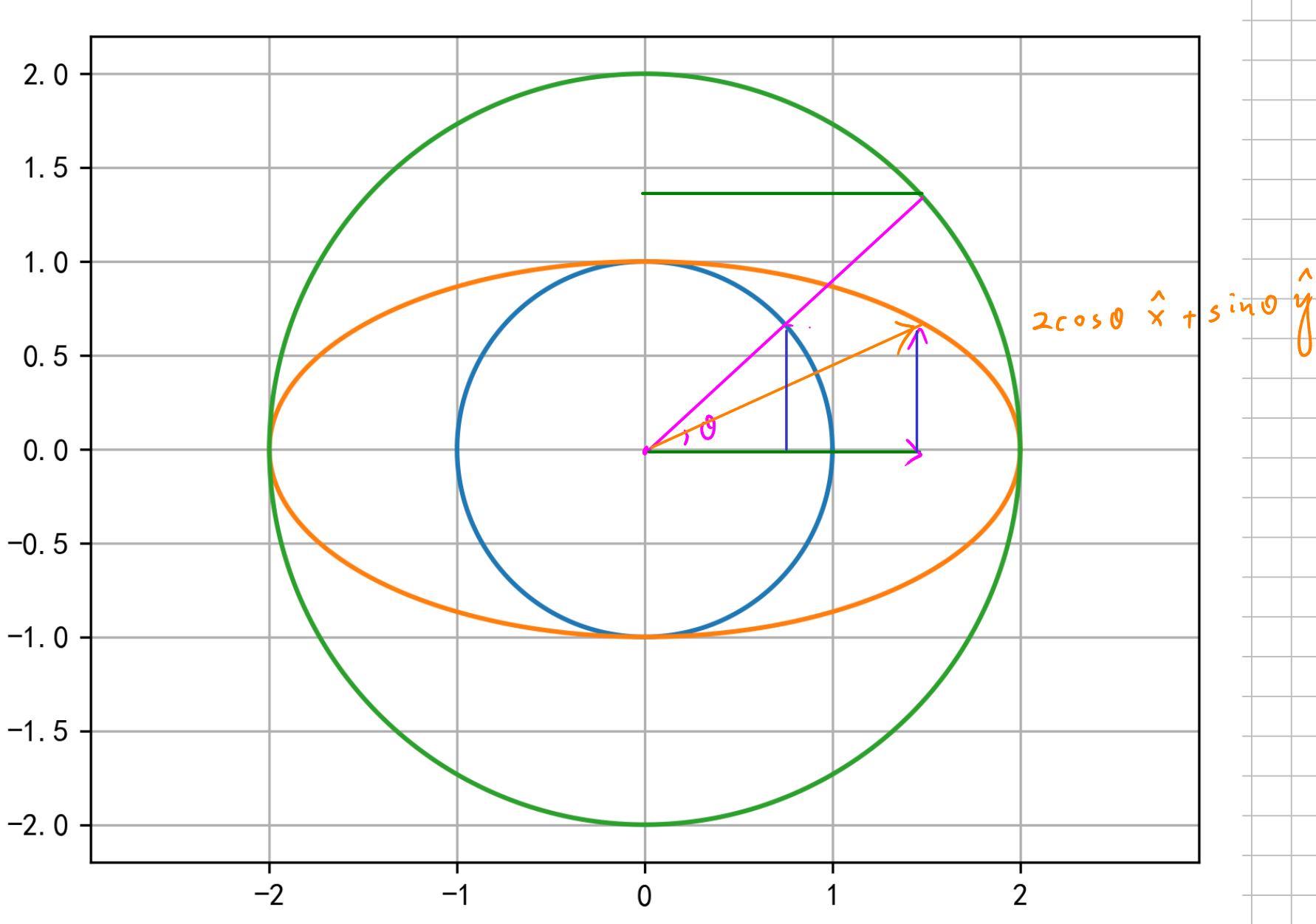
可以通过拉伸坐标使使得相图变成一个圆,那么就可以用一个角度 $\theta = \omega t$ 和一个半径 $I$ 来表示圆上的任意一点,其中 $I$ 具有角动量的量纲。
相图上圆的半径是不变的,当弹簧 $x =x_0$ 势能取最大,$E = m x_0^2 \omega^2 / 2$ 可以证明 $$I = \frac {1} {2\pi} \oint p dx = E/\omega$$ 是守恒量。
产生湮灭算符
利用欧拉公式,式 (1) 和 (2) 还可以写成 $$x=x_0 \cos \omega t = x_0 \left( \frac{e^{i \omega t} + e^{-i \omega t}}{2} \right)$$ 和 $$p=-mx_0 \omega \sin \omega t = -mx_0 \omega \left( \frac{e^{i \omega t} - e^{-i \omega t}}{2i} \right)$$
这给我们启示,位置和动量作为两个实数(两个自由度)可以写成一对共轭复数的叠加(一个复数有两个自由度); 从几何上看,是两个反方向圆周运动的叠加。 定义产生、湮灭算符 $a^\dagger$、$a$ 为
$$\hat{x} = \frac{1}{\sqrt{2m\omega}} (a + a^\dagger)$$
$$\hat{p} = \frac{-i m\omega}{\sqrt{2m\omega}} (a - a^\dagger)$$
由 Canonical commutation relation $$[\hat{x}, \hat{p}] = i,$$ 可以推出湮灭、产生算符的对易关系 $$[\hat{a}, \hat{a}^\dagger] = 1.$$
在粒子数表象,产生湮灭算符有如下性质: $$\hat{a} \ket{n} = \ket{n-1}$$
$$\hat{a}^\dagger \ket{n} = \ket{n+1}$$
$$\hat{N} \ket{n} = n \ket{n}$$
例:求真空态的波函数 $\langle x | 0 \rangle$
解: 在 $x$ 表象下 $$\langle x| a| 0 \rangle = 0$$ 即 $$\left\langle x\middle| \hat{x} + \frac{i\hat{p}}{m \omega} \middle| 0 \right\rangle = 0$$ 向左作用 $$\left(x + \frac{i}{m\omega} (-i) \frac{\mathrm{d} }{\mathrm{d} x}\right) \langle x|0\rangle=0$$ 解此常微分方程得: $$\langle x|0\rangle = C e^{-m\omega x^2 / 2}$$