..
用 Julia 画 koch snowflake
仿照 matplotlib 文档 画了 Koch snowflake:
using PyCall
@pyimport matplotlib.pyplot as plt
"""
[x2, x3, x1] - [x1, x2, x3]
"""
function diff1(x::Vector)::Vector
y = similar(x)
for i in 1:length(x)-1
y[i] = x[i+1] - x[i]
end
y[end] = x[1]-x[end]
return y
end
function koch_snowflake_complex(order::Int)::Vector{ComplexF64}
if order == 0
pos = @. 10/sqrt(3) * exp(deg2rad([0, 120, 240]+90)*im)
else
p = koch_snowflake_complex(order-1)
dp = diff1(p)
ZR = ℯ^(-(π/6)im) * sqrt(3)/3
pos=similar(p, length(p)*4)
pos[1:4:end] = p
pos[2:4:end] = @. p + dp/3
pos[3:4:end] = @. p + dp * ZR
pos[4:4:end] = @. p + dp/3*2
end
return pos
end
function main()
pos=koch_snowflake_complex(3)
x = real.(pos)
y = imag.(pos)
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(9, 3),
subplot_kw=Dict(:aspect=>"equal"))
ax1.fill(x, y)
ax2.fill(x, y, facecolor="lightsalmon", edgecolor="orangered", linewidth=3)
ax3.fill(x, y, facecolor="none", edgecolor="purple", linewidth=3)
plt.savefig("$(bytes2hex(rand(UInt8, 4))).png", bbox_inches="tight")
plt.show()
end
main()
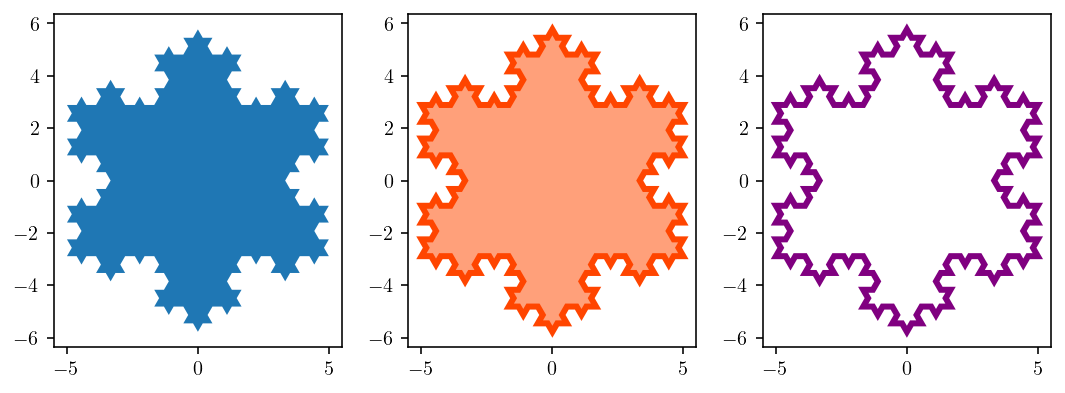
逛论坛发现早有人用6行干了同样的事情, sigh.