..
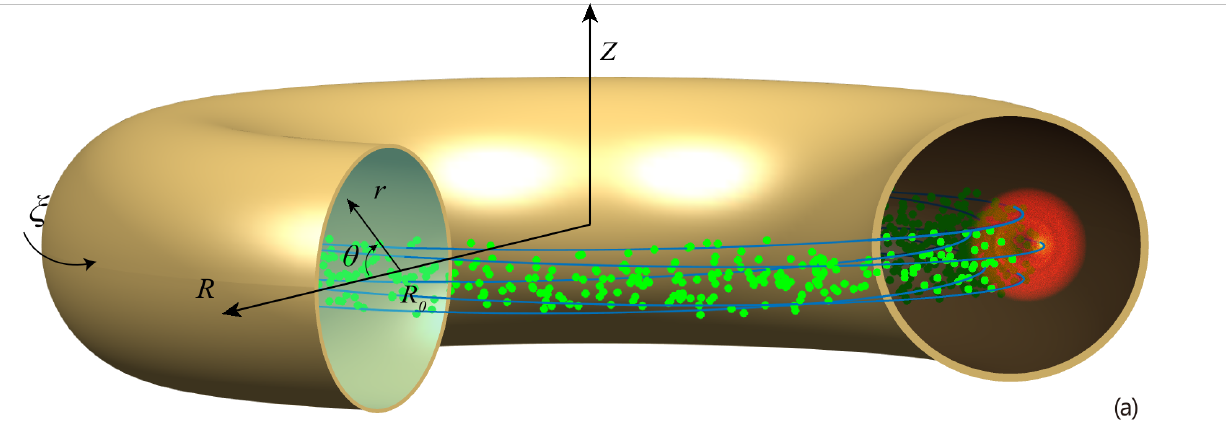
toroidal and poloidal coordinates
$\require{physics}$
$$\begin{equation} \sin \zeta = -\frac{y}{R} \quad \cos \zeta = \frac{x}{R} \end{equation}$$
$$\begin{aligned} \vu{\zeta} = -\sin \zeta \vu{x} - \cos \zeta \vu{y}, \\ \vu{\theta} = - \sin \theta \vu{R} + \cos \theta \vu{z}\\ \vu{R} = \cos \zeta \vu{x} - \sin \zeta \vu{y}. \end{aligned}$$From the above equations, it can be concluded that $$\begin{equation} \vu{\theta} = - \sin \theta \cos \zeta \vu{x} + \sin \theta \sin \zeta \vu{y} + \cos \theta \vu{z}. \end{equation}$$